Theorems of Perpendicular and Parallel Axes

The parallel axis theorem uses the _____ of the distance.

The moment of inertia of a hollow cubical box of mass $M$ and side length $a$, about an axis passing through centres of two opposite faces, is equal to $\frac{xM{a}^2}{18}$. The value of $x$ is

The moment of inertia of a hollow cubical box of mass $M$ and side length $a$, about an axis passing through centres of two opposite faces, is equal to $\frac{xM{a}^2}{18}$. The value of $x$ is

The moment of inertia of a thin rod of length $L$ and mass $M$ about an axis passing through a point at a distance $\frac{L}{3}$ from one of its ends and perpendicular to the rod is,

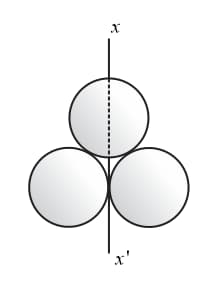
Three solid spheres of mass $M$ and radius $R$ are shown in the figure. The moment of inertia of the system about $xx\text{'}$ axis will be,

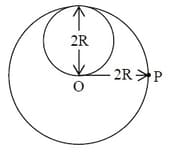
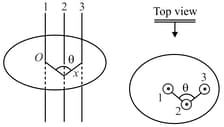
A lamina is made by removing a small disc of diameter $2\mathrm{R}$ from a bigger disc of uniform mass density and radius $2\mathrm{R}$, as shown in the figure. The moment of inertia of this lamina about axes perpendicular to the plane of the lamina and passing through the points $\mathrm{O}$ and $\mathrm{P}$ is ${\mathrm{I}}_{\mathrm{O}}$ and ${\mathrm{I}}_{\mathrm{P}}$​ respectively. If the ratio $\frac{{\mathrm{I}}_{\mathrm{P}}}{{\mathrm{I}}_{\mathrm{O}}}=\frac{\mathrm{m}}{\mathrm{n}}$, where $\mathrm{m}$ and $\mathrm{n}$ are the smallest integers, then what is the value of $\mathrm{m}+\mathrm{n}$?

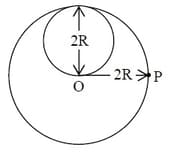
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure.The moment of inertia of this lamina about axes passing though O and P is I_O and I_P​ respectively. Both of these axes are perpendicular to the plane of the lamina.The ratio I_P / I_O to the nearest integer is 

State and prove principle of perpendicular axes.

State and prove principle of parallel axes.

A uniform disc of radius R lies in the $x-y$ plane, with its center at origin. Its moment of inertia about $z$-axis is equal to its moment of inertia about line$y=x+c.$ The value of $c$will be

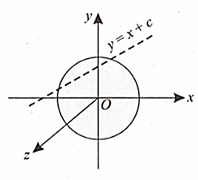
With reference to figure of a cube of edge $a$ and mass $m$ . which of the following is the incorrect statement?
( $O$ is the centre of the cube)

A square frame $ABCD$ is formed by four identical rods each of mass '$m$ ' and length '$l$ '. This frame is in $X-Y$ plane such that side $AB$ coincides with X-axis and side $AD$ along Y-axis. The moment of inertia of the frame about X-axis is

$1$, $2$ and $3$ are three axes perpendicular to the plane of a disc. $X$ is the distance between axes $2$ and $3$. Find $\mathrm{\theta }$ for which $I_3=I_2+m{x}^2$

($O$ is the centre of mass of the disc and $I$ stands for a moment of inertia)

The moment of inertia of a hollow cubical box of mass $M$ and side length $a$, about an axis passing through centres of two opposite faces, is equal to $\frac{xM{a}^2}{18}$. The value of $x$ is

The moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the center of mass and perpendicular the to the axis of the cylinder is ${\mathrm{I1}}_{}$ and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is $I_2$ , then

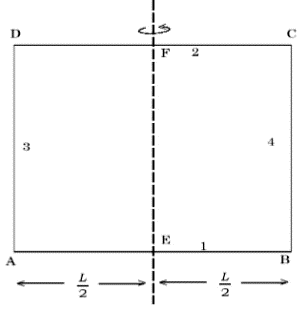
Four thin metal rods, each of mass $M$ and length $L$, are welded to form a square $ABCD$ as shown in the figure. The moment of inertia of the composite structure about a line that bisects rods $AB$ and $CD$ is

Three identical rods each of length ' $l$ ' are joined to from a rigid equilateral triangle. Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is

Figure shows a sphere of mass $M$ and radius $R$. Let $AA\text{'}$ and $BB\text{'}$ be two axis as shown in the figure. Then -



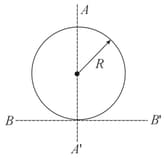
Assertion: Parallel axis theorem is not applicable between axis $A{A}^{\mathrm{\prime }}$ and $B{B}^{\mathrm{\prime }}$

Reason: $I_{\mathit{B}{\mathit{B}}^{\mathit{\prime }}}= I_{\mathit{A}{\mathit{A}}^{\mathit{\prime }}}+\mathrm{ }M{R}^2$

The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is $I_0$. What is the M.I. about an axis through one end and perpendicular to the rod?

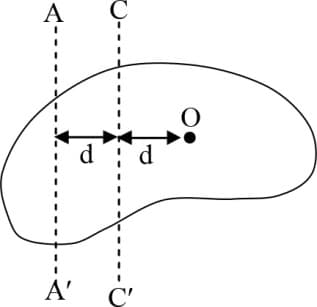
The figure shows a body of arbitrary shape '$O$' is the center of mass of the body and mass of the body is $M$. If $I_{\mathrm{C}{\mathrm{C}}^{\text{'}}}=I_0$ then $I_{{\mathrm{AA}}^{\text{'}}}$ will be equal to